7 4 Divided By 2
Dividing Fractions
We will discuss here about dividing fractions past a whole number, by a partial number or past another mixed fractional number.
First let us recall how to find reciprocal of a fraction, we interchange the numerator and the denominator.
| For instance, the reciprocal of ¾ is iv/3. | |
Notice the reciprocal of 3 ¾
| The reciprocal of iii ¾ is 4/15. | |
I. Division of a Fraction by a Whole Number:
4 ÷ 2 = 2 means, there are ii 2's in iv.
6 ÷ 2 = 3 means, at that place are two 2'southward in 6.
Similarly 5 ÷ \(\frac{1}{2}\) ways, how many halves are there in v?
We know that \(\frac{i}{2}\) + \(\frac{1}{2}\) = ane
| \(\frac{i}{2}\) + \(\frac{one}{ii}\)+ | \(\frac{1}{2}\) + \(\frac{1}{2}\)+ | \(\frac{1}{2}\) + \(\frac{i}{2}\)+ | \(\frac{one}{2}\) + \(\frac{1}{2}\)+ | \(\frac{i}{two}\) + \(\frac{ane}{2}\) | |
| i+ | 1+ | i+ | 1+ | 1 | = 5 |
i.e. at that place are 10 halves in 5.
5 ÷ \(\frac{i}{two}\) = 5 × \(\frac{two}{1}\) = \(\frac{10}{ane}\) = 10
For Example:
ane. \(\frac{vii}{10}\) ÷ 5 = \(\frac{7}{ten}\) ÷ \(\frac{5}{1}\)
= \(\frac{7}{10}\) × \(\frac{i}{five}\)
= \(\frac{7 × 1}{10 × 5}\)
= \(\frac{7}{50}\)
| 2. What is \(\frac{10}{15}\) ÷ 5? \(\frac{10}{15}\) ÷ \(\frac{v}{ane}\) = \(\frac{10}{15}\) × \(\frac{1}{5}\) = \(\frac{ii × \not 5 × ane}{three × \not 5 × 5}\) = \(\frac{2}{fifteen}\) | 10 = two × 5 15 = 3 × v 5 = 1 × v |
To divide a fraction past a number, multiply the fraction with the reciprocal of the number.
For instance:
3. Dissever three/five past 12
| Solution: three/5 ÷ 12 = three/5 ÷ 12/1 = 3/5 × one/12 = (iii × one)/(v × 12) = 3/sixty = 1/xx | Step I: Discover the reciprocal of the whole number and multiply with the partial number as usual. Step Two: Express the product in its lowest terms. |
4. Solve: 5/7 ÷ x
| = 5/7 ÷ 10/1 = 5/7 × one/10 = (5 × i)/(7 × x) = 5/lxx | Step I: Notice the reciprocal of the whole number and multiply with the partial number as usual. Step II: Express the product in its lowest terms. |
II. Division of a Partial Number by a Fractional Number:
For example:
1. Divide seven/8 past one/5
| Solution: 7/eight ÷ 1/5 = 7/8 × 5/1 = (vii × 5)/(8 × 1) = 35/8 = 4 iii/8 | Step I: Discover reciprocal of 1/5. Step II: Multiply seven/eight past information technology. Step III: Express the product in its simplest form. |
2. Split: five/nine ÷ 10/18
| Solution: v/9 ÷ ten/18 = 5/9 × 18/10 = (5 × 18)/(9 × 10) = 90/ninety = one | Step I: Find reciprocal of one/5. Stride II: Multiply 7/8 by information technology. Pace III: Express the product in its simplest form. |
Sectionalisation of a Fraction past a Fraction:
3. Divide \(\frac{3}{iv}\) ÷ \(\frac{5}{3}\)
Step I: Multiply the first fraction with the reciprocal of the second fraction.
Reciprocal of \(\frac{v}{three}\) = \(\frac{3}{5}\)
Therefore, \(\frac{three}{4}\) ÷ \(\frac{5}{iii}\) = \(\frac{iii}{4}\) × \(\frac{3}{v}\)
= \(\frac{three × iii}{4 × 5}\)
= \(\frac{ix}{20}\)
Step II: Reduce the fraction to the lowest terms. (if necessary)
| 4. Divide \(\frac{xvi}{27}\) ÷ \(\frac{4}{9}\) Therefore, \(\frac{16}{27}\) ÷ \(\frac{iv}{9}\) = \(\frac{16}{27}\) × \(\frac{nine}{4}\); [Reciprocal of \(\frac{4}{9}\) = \(\frac{9}{4}\)] = \(\frac{\not two × \not 2 × 2 × two × \non 3 × \not 3}{\not 3 × \not 3 × 3 × \not 2 × \not two}\) = \(\frac{iv}{3}\) = 1\(\frac{1}{iii}\) | 16 = two × 2 × ii × 2 9 = iii × 3 27 = 3 × 3 × 3 iv = 2 × 2 |
III. Division of a Mixed Number past some other Mixed Number:
For example:
i. Dissever two ¾ by ane two/3
| Solution: 2 ¾ ÷ one ii/3 = 11/4 ÷ v/3 = xi/four × 3/5 = (11 × 3)/(4 × 5) = 33/20 = ane 13/20 | Express the mixed numbers as improper fractions and multiply as usual. |
ii. Divide: 2 4/17 ÷ i four/17
| Solution: two iv/17 ÷ 1 4/17 = 38/17 ÷ 21/17 = 38/17 × 17/21 = (38 × 17)/(17 × 21) = 646/357 = 38/21 = 1 17/21 | Express the mixed numbers equally improper fractions and multiply as usual. |
Questions and Answers on Dividing Fractions:
I. Divide the following.
(i) \(\frac{2}{half dozen}\) ÷ \(\frac{1}{iii}\)
(two) \(\frac{v}{8}\) ÷ \(\frac{15}{16}\)
(three) \(\frac{5}{6}\) ÷ 15
(four) \(\frac{7}{8}\) ÷ 14
(v) \(\frac{2}{iii}\) ÷ 6
(half-dozen) 28 ÷ \(\frac{7}{4}\)
(vii) 2\(\frac{v}{half-dozen}\) ÷ 34
(8) 9\(\frac{one}{ii}\) ÷ \(\frac{38}{two}\)
(9) 3\(\frac{one}{4}\) ÷ \(\frac{26}{28}\)
(ten) vii\(\frac{1}{3}\) ÷ 1\(\frac{v}{six}\)
(eleven) 2\(\frac{3}{5}\) ÷ 1\(\frac{eleven}{15}\)
(xii) one\(\frac{ane}{2}\) ÷ \(\frac{4}{7}\)
Related Concept
● Fraction of a Whole Numbers
● Representation of a Fraction
● Equivalent Fractions
● Properties of Equivalent Fractions
● Similar and Dissimilar Fractions
● Comparison of Like Fractions
● Comparison of Fractions having the aforementioned Numerator
● Types of Fractions
● Irresolute Fractions
● Conversion of Fractions into Fractions having Same Denominator
● Conversion of a Fraction into its Smallest and Simplest Form
● Addition of Fractions having the Aforementioned Denominator
● Subtraction of Fractions having the Same Denominator
● Improver and Subtraction of Fractions on the Fraction Number Line
4th Grade Math Activities
From Dividing Fractions to Domicile Page
Didn't find what you lot were looking for? Or desire to know more information well-nigh Math But Math. Use this Google Search to discover what yous need.
7 4 Divided By 2,
Source: https://www.math-only-math.com/dividing-fractions.html
Posted by: bowenrusuremb.blogspot.com

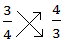
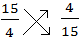


0 Response to "7 4 Divided By 2"
Post a Comment